Andre problemer knyttet til brøk
Mange elever identifiserer brøk med å beherske regler og prosedyrer. De skiller ikke mellom forståelse av begrepet brøk – hvilke ideer som er knyttet til begrepet – og algoritmene.
I arbeid med brøk er det viktig å presisere hvilket aspekt av brøkbegrepet det arbeides med.
En av de grunnleggende ideene elevene må forstå, er at selv om en brøk består av teller og nevner, representerer brøken ett tall, på samme måte som for eksempel de hele tallene. Når brøk blir betraktet som en tallstørrelse, har den også sin plass på tallinja (rasjonalt tall). De fleste elever vil plassere `(1)/(2)` riktig på tallinja, dersom den strekker seg fra 0 til 1. Strekker talllinja seg ut over 0 og 1, som vist i figur 1, vil en del elever få problemer. Noen svarer at `(1)/(2)` skal stå på punktet 0, fordi det er halvparten av linja (brøk som operator). Andre svarer at `(1)/(2)` skal stå mellom 1 og 2, fordi tallene 1 og 2 er med i brøken (heltallstenking). I tillegg vil enkelte elever si at `(1)/(2)` kan stå hvor som helst på tallinja. Det siste stemmer dersom det er snakk om brøk som måltall, da kan lengden «en halv» merkes av hvor som helst på tallinja, for eksempel linjestykket fra 1 til 1,5.

Figur 1 Eksempel på tallinje
Heltallstenking kan også føre til at enkelte elever tenker at det ikke kan være noen brøk mellom for eksempel 0 og 1, for det er ingen hele tall mellom 0 og 1.
Elevenes manglende forståelse av brøk kommer til syne når de skal regne med brøk. En del av dem vil overgeneralisere regneregler de bruker i arbeid med hele tall.
Den vanligste misoppfatningen knyttet til addisjon og subtraksjon med brøk er at elevene betrakter telleren og nevneren som to uavhengige hele tall, i stedet for ett tall som angir del–hel. De adderer eller subtraherer de to tellerne og de to nevnerne uavhengig av hverandre. Eksempel: `(1)/(2) + (3)/(4) = (4)/(6)`, fordi 1 + 3 = 4 og 2 + 4 = 6.
Ved å reflektere rundt brøker som størrelser vil elevene erfare at denne tenkningen ikke fører fram til riktig svar. I dette eksemplet er begge brøkene en halv eller mer, så elever som har forstått brøk, vil se at summen må bli mer enn en hel.
Misoppfatninger kan oppstå eller bli forsterket gjennom enkelte representasjoner. Dersom addisjon og subtraksjon av to brøker for eksempel blir representert ved hjelp av to rektangler, som i figur 2, er det sannsynlig at noen elever vil svare at `(2)/(5) + (1)/(5) = (3)/(10)`. Elevene ser tre blå deler av totalt ti deler, og tenker `(3)/(10)` som svar i stedet for `(3)/(5)`. I oppgaven `(2)/(5) + (1)/(5)` dreier det seg om to brøker av samme helhet, og ikke to ulike helheter, slik figur 2 legger opp til.
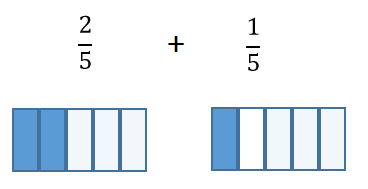
Figur 2 Representasjon av brøkene hver for seg
Addisjon kan også representeres med ett rektangel. Da blir brøkene representert i samme helhet, som figur 3 viser.
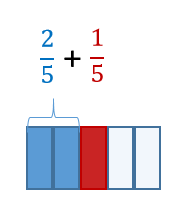
Figur 3 Representasjon av brøker som deler av samme helhet
Tallinja vil for noen være en bedre representasjon i denne oppgaven, men den er samtidig mer abstrakt og kan dermed være vanskeligere å forstå, se figur 4.
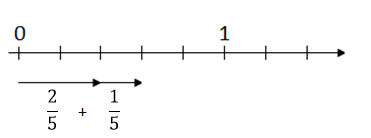
Figur 4 Representasjon av addisjon, der brøkene er lagt etter hverandre på tallinja
Elevene bør møte brøkbegrepet og operasjoner med brøk gjennom ulike representasjoner. Alle tre representasjonene over viser addisjon av brøk. En må bare være bevisst på å understreke hva som er helheten i de ulike representasjonene.
I arbeid med brøk er det altså viktig å presisere hvilket aspekt av brøkbegrepet en arbeider med. I oppgaver med addisjon og subtraksjon er det underforstått at det er dreier seg om aspektet brøk som del av samme helhet (del – hel). Dersom elevene tolker rektanglene i figur 2 som forhold (del–del), kan de tenke at to femdeler av det ene rektanglet og en femdel av det andre rektanglet blir til sammen tre deler av i alt ti deler. Da blir svaret `(3)/(10)` fordi delene til sammen utgjør en ny helhet. Denne tenkingen fører til at `(2)/(3)` og `(3)/(5)` til sammen blir `(5)/(8)`.
Enkelte elever ignorerer nevnerne i brøkene, og forholder seg bare til tellerne. De adderer (eller subtraherer) tellerne og beholder den største nevneren. Eksempel: `(1)/(2) + (3)/(4) = (4)/(4)`, fordi
1 + 3 = 4, og den største nevneren er 4.
For en del elever er matematikk mange symboler som skal manipuleres etter bestemte regler. Usikkerhet og sammenblanding av regler bidrar til feil. Dersom elevene har god forståelse av brøk, vil de være i stand til å vurdere svaret sitt og oppdage at det er feil, for eksempel svaret i figur 5. Et overslag vise at svaret her må bli større enn 3.

Figur 5 Eksempel på sammenblanding av regler i addisjon av blandede tall
Multiplikasjon og divisjon av brøk, rent mekanisk, er enkelt. I multiplikasjon er huskeregelen multiplisere teller med teller og nevner med nevner, og i divisjon snu den bakerste brøken og multiplisere. Når reglene er så enkle, er det mer fristende å bare pugge dem enn å prøve å forstå hvorfor de virker. Bruk av reglene alene gir ikke elevene innsikt i om løsningen de får, er rimelig. For å kunne løse oppgavene må de stole på hukommelsen. Det kan ofte føre til feil svar. Elevene kan for eksempel blande reglene for addisjon og multiplikasjon. De bruker «multiplikasjonsregelen» i addisjon og glemmer hvilken brøk de skal snu i divisjon. Figur 6 viser eksempler på elever som er usikre på reglene. De adderer teller med teller og nevner med nevner, og snur den første brøken i divisjon.

Figur 6 Eksempel på usikkerhet knyttet til regler og prosedyrer
Å multiplisere to brøker er lettere enn å addere, det er bare å multiplisere teller med teller, og nevner med nevner. Ved å drille regler er det fare for å miste forståelsen. Når begge faktorene er brøker, kan elevene få riktig svar med feil tenking (de ser på teller og nevner som to hele tall, uten å vurdere relasjonen mellom dem). Problemer kan oppstå når eleven skal multiplisere et heltall med brøk. Eksempel: `7 · (1)/(2) = (7)/(14)`. Eleven multipliserer heltallet med både telleren og nevneren.
Elever som tenker at multiplikasjon gjør svaret større, kan oppleve at svaret de får, ikke stemmer med denne forestillingen. I oppgaver der brøk inngår, kan disse elevene prøve å snu brøken for å få et svar som er større.
Forkorting av brøker kan føre til problemer for en del elever, enten underveis i prosessen eller i svaret. Regelen stryke over samme tall skaper mye usikkerhet og gjetting i brøkregning, se figur 7.
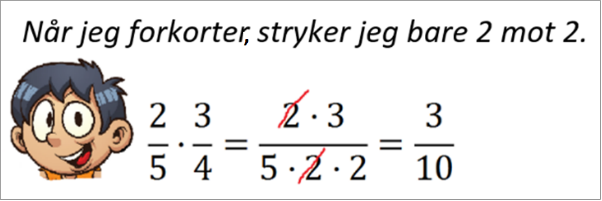
Figur 7 Eksempel på bruk av regel
Noen elever vil i dette eksemplet stryke 2-tallet i telleren og begge 2-tallene i nevneren. I stedet for å si stryk 2 i telleren og nevneren bør en fokusere på bruk av identitetselementet i multiplikasjon. Å multiplisere med 2 i både telleren og nevneren er egentlig det samme som å multiplisere brøken med tallet `1(1)/(2)`. Å multiplisere med 1 endrer ikke verdien.
Bruken av inverse tall og inverse regnearter kan være til hjelp i arbeidet med divisjon med brøk. Inverse operasjoner med inverse tall gir samme resultat. Eksempler: `(2)/(3)` og `(3)/(2)`
er inverse tall, multiplikasjon og divisjon er inverse operasjoner. Det er grunnen til at en i divisjon med brøk kan snu den bakerste brøken og multiplisere.
For elever som lærer brøk gjennom regler, blir det mange og vanskelige regler å holde atskilt. Elevene opplever da at regning med brøk er triksing med regler for å få et svar som virker riktig, ut fra deres erfaringer. Dersom de har misoppfatninger, kan triksingen være et grep for å få svar som stemmer overens med disse misoppfatningene. Arbeid med begrepsforståelse av brøk og regning med brøk er tidkrevende. Men i sum vil det være tidsbesparende å arbeide så grundig at elevene forstår det de gjør.
Oppgaver
I prøven Misoppfatninger knyttet til brøk og prosent er det seks oppgaver innen denne kategorien. Fire av oppgavene er med i prøven for 5.–7. trinn, og fem oppgaver er med i prøven for 8.–10. trinn. Tre av oppgavene ser du nedenfor.
Analyse

Oppgave 20 utfordrer elevene som er i heltallstenking, ved at de skal velge en brøk som har verdi mellom 0 og 1. Som elevsvarene nedenfor viser, får disse elevene problemer, siden de ikke finner noe heltall mellom 0 og 1. Det vil derfor oppleves som umulig å lage en brøk med verdi mellom 0 og 1. Resultatet av analysene viser at dette gjelder 40 % av elevene, både på 6. og 9. trinn.
Elever som svarer `(0)/(1)` tenker trolig ikke over at en brøk har en verdi, men tar bare tallene fra oppgaven og skiller dem med en brøkstrek.
I oppgave 5 i prøven for 5.–7. trinn og oppgave 16 i prøven for 8.–10. trinn skal elevene regne med brøk. I oppgave 5 skal de addere to brøker med samme nevner, `(2)/(4)` og `(5)/(4)`. Resultatet av analysene tyder også her på at mange elever er i heltallstenking, i og med at 44 % av elevene på 6. trinn adderer teller med teller og nevner med nevner og svarer `(7)/(8)`. I oppgave 16 skal elevene regne ut `(1)/(4) : 2`, altså halvparten av `(1)/(4)`. Elevsvarene nedenfor tyder på at mange prøver å huske en regel for divisjon med brøk, men at de enten husker feil, eller at de møter problemer fordi det er brøk og heltall og ikke brøk og brøk i oppgaven. Elevsvarene `(8)/(1)` og `(8)/(2)` er tydelige eksempler på det. I tillegg viser det at elevene enten har veldig lav brøkforståelse eller i alle fall reflekterer svært lite over svaret sitt.
Elevsvar
Nedenfor er noen elevsvar fra da oppgavene ovenfor ble testet ut på papir, uten svaralternativer. Svarene er gitt av elever fra 5. til 10. trinn.