Pytagoras setning

Emne
Lengder, vinkler, areal, formlikhet og pytagoras setning
Dette opplegget er hentet fra heftet: "Undersøkende matematikk - undervisning i videregående skole"
Hensikt
• Å forstå et visuelt bevis for Pytagoras setning
• Å kunne gjennomføre et bevis
• Å kunne beregne lengder i rettvinklede trekanter ved hjelp av Pytagoras setning
Du trenger
Sett som inneholder tre gjennomsiktige plastesker med fargede brikker. Disse kalles «Pythagorean Theorem og kan bestilles på nett. Kvadrater i farget papir (se detaljert forklaring i beskrivelsen av opplegget).
Beskrivelse av opplegg
Forberedelser
I dette opplegget skal vi bruke esken i midten på figur 1. Til hvert sett: Klipp ut et kvadrat i rødt papir
som passer nøyaktig inn i esken. Legg det inn i bunnen av esken. Legg så tilbake de fire gule trekantene og det blå pappkvadratet som ligger i midten. Hvis det ikke ligger noe blått kvadrat i midten (kvadrat på hypotenusen), må slike også klippes ut og legges inn.
Undervisningsopplegget
På de neste sidene blir oppgavene til dette undervisningsopplegget presentert med kommentarer til læreren. Opplegget inneholder et visuelt «bevis» for Pytagoras setning. Det er mangelfullt som bevis, men likevel ganske overbevisende.
Grunnen til at dette ikke er noe fullgodt bevis, er at vi påstår at vi får kvadrater, uten å vise hvorfor det virkelig er slik.
Opplegget er helt «algebrafritt» i pkt. 1–5. Målet er at elevene skal se hvordan de kan løse oppgaver med Pytagoras setning uten å bruke algebra og løse likninger. Det er nok å ha en figur til hjelp. For en del elever er det et rimelig læringsmål. Det er viktig at også elever som behersker algebra godt, får med seg denne måten å tilnærme seg Pytagoras setning på.
I pkt. 6 innføres bokstaver som navn på sidene, og vi ender med den kjente formelen for Pytagoras setning: a2 + b2 = c2.
Introduksjon av undervisningsopplegget
Be elevene skrive opp alt de husker om rettvinklede trekanter og Pytagoras setning. Ta det opp i fellesskap, hør hva elevene allerede kan, og bruk anledningen til å supplere og korrigere eventuelle misforståelser.
1 Begynn med esken der brikkene ligger, slik:

Kommentar til læreren
Det ligger et blått pappkvadrat inne i eskene. Hvis dette mangler, bør det legges et slikt kvadrat inn i eskene.
a Hvorfor kaller vi de fire trekantene for rettvinklede trekanter? Skriv med egne ord.

b Den blå firkanten i midten er et kvadrat, vi kaller den kvadratet på hypotenusen. Hvorfor? Skriv og forklar.

De resterende oppgavene finner du i kopieringsoriginalene.
f Hva kan vi si om arealet av det store blå kvadratet i forhold til arealene av de to røde kvadratene? Regelen du har funnet, kalles Pytagoras setning. Skriv regelen i ruta nedenfor.

Kommentar til læreren
La elevene arbeide seg gjennom pkt. a, hvor de skal prøve å formulere skriftlige svar i alle rutene. Læreren kan benytte anledningen til å se hvordan enkeltelever arbeider, og det er mulighet til å ha små samtaler med dem.
Når elevene er ferdig med dette punktet, bør læreren stoppe opp og samtale med elevene i plenum. Hva har de skrevet? Hvorfor har de skrevet det slik? Det er mange måter å uttrykke seg på, og alle utsagn som er riktige, må verdsettes. Mange elever fanger opp gode tips og ideer fra andres forklaringer. Det er like viktig å kunne være god til å lytte som å være god til å forklare. Samtidig er dette en anledning for læreren til å fange opp og avklare misforståelser.
Hensikten med opplegget er at elevene skal forstå hva Pytagoras setning egentlig sier om rettvinklede trekanter og kvadratene på sidene. Det er fint om de formulerer setningen i pkt. f med ord, for eksempel «Arealet av det blå kvadratet er like stort som arealene av de røde kvadratene til sammen» eller «Arealet av kvadratet på hypotenusen er like stort som
arealet av kvadratene på katetene til sammen».
2 Eksempel:
Vi tenker oss at alle de rettvinklede trekantene har en katet som har lengde 3, en katet som har lengde 4, og hypotenus med lengde 5.
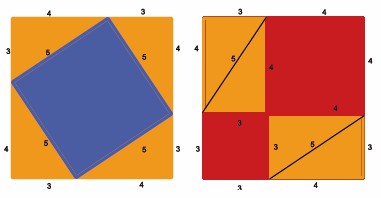
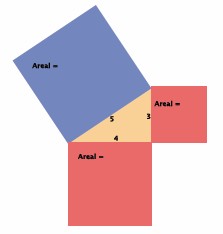
a Hvor stort er arealet av det blå kvadratet i dette tilfellet?
b Hvor store er arealene av de to røde kvadratene?
c Stemmer regelen til Pytagoras i dette tilfellet? Skriv og forklar.
Kommentar til læreren
Stans etter pkt. 2 og hør hva elevene har kommet fram til her. Diskusjon/samtale. Har elevene forstått sammenhengen mellom de to figurene?
Noen elever bør kanskje stanse etter pkt. 5 og fortsette å løse Pytagoras-problemer med den metoden de har lært. I pkt 6. tar vi i bruk algebra og symboler, og elever som er modne for det må selvsagt bruke algebra. Men med dette opplegget ønsker vi at elevene skal få en bedre forståelse av hva som ligger bak Pytagoras setning, slik at de ikke bare bruker en regel helt mekanisk.
Når du samtaler om løsninger med elever, så spør «Hvorfor gjør du slik?» eller «Hva har du gjort her?» for å få tak i hva eleven har tenkt. Slike spørsmål bør man også stille til elever som ser ut til å løse alle oppgavene uten problemer.
Sørg for å avslutte økta og oppsummere begrepene og læringsmålene.
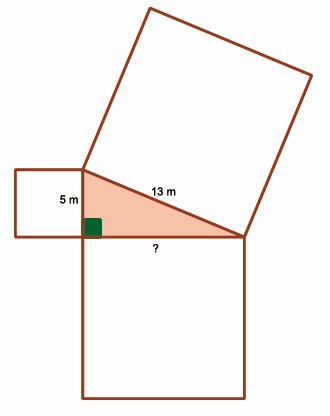
5 Hypotenusen i en rettvinklet trekant er 13 m lang, og den korteste kateten er 5 m. Hvor lang er den andre kateten?
Kommentar til læreren
Noen elever bør kanskje stanse etter pkt. 5 og fortsette å løse Pytagoras-problemer med den metoden de har lært.
I pkt. 6 tar vi i bruk algebra og symboler, og elever som er modne for det, må selvsagt bruke algebra. Med dette opplegget ønsker vi at elevene skal få en bedre forståelse av hva som ligger bak Pytagoras setning, slik at de ikke bare bruker en regel helt mekanisk.
Sørg for å avslutte økta og oppsummere begrepene og læringsmålene.
Kompetansemål
